Invited Speakers:

1. -Giorgio Ottaviani (Università di Firenze)
   

2. -Hwang, Jun-Muk (KIAS)
   

3. -Ahn, Jeaman (Kongju National University)
   

4. -Mounir Nisse (KIAS)
   

5. -Cristiano Bocci (Università di Siena)
   

Organizers:

1. -Keum, JongHae (Korea Institute for Advanced Study, KIAS)
   

2. -Choe, Insong (Konkuk University)
   

3. -Han, Kangjin (Korea Institute for Advanced Study, KIAS)
   

1. *For registration and inquires, please send an e-mail (including name, institution, position, contact(e-mail), and banquet(yes/no) ) to Han, Kangjin (kangjin.han at kias dot re dot kr).
   

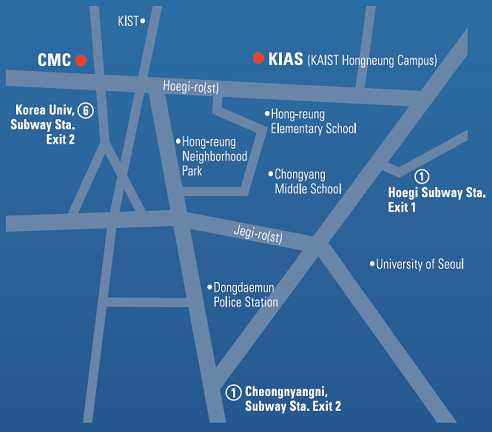
Place: Room 403, Center for Mathematical Challenges (CMC)

Video archive! (click here)

Workshop Photos!! (click here)

Schedule:

10:00-10:50  Ottaviani

10:50-11:10  Break

11:10-12:00  Hwang

12:00-14:00  Lunch

14:00-14:50  Ahn

14:50-15:10  Break

15:10-16:00  Nisse

16:00-16:20  Break

16:20-17:10  Bocci

                     Banquet

Talks:

1. -G. Ottaviani, "Expressing a polynomial of degree kd as sum of k-th powers"
   

- J-M. Hwang, "Minimal rational curves on Veronese double cones"

1. -J. Ahn, "Degree Complexity: How difficult is it to compute Groebner bases?"
   

2. -M. Nisse, "A tropical characterization of an analytic variety to be algebraic"
   

3. -C. Bocci, "m-dissimilarity tensors and graphs of genus 1"
   

Abstracts:

"Expressing a polynomial of degree kd as sum of k-th powers" by Ottaviani (FOS beamer.pdf).

: Any homogeneous polynomial of degree $kd$ can be expressed as a sum of $k$-th powers of homogeneous polynomials of degree $d$. A natural question is to compute the minimal number of summands which are needed to express in this way a general polynomial. In the case $d=1$ the answer has been given by a celebrated theorem by Alexander and Hirschowitz, in 1995. The case $k=1$ being trivial, the case $k=2$ leads to interesting questions for polynomials which can be written as sum of squares. We exhibit a upper bound on the number of needed summands, which is asymptotically sharp for any fixed $k$ and $d$ going to infinity, obtained in collaboration with R. Froberg and B. Shapiro.

"Minimal rational curves on Veronese double cones" by Hwang.

: A rational curve $C$ in a nonsingular variety $X$ is standard if under the normalization $f: \mathbb{P}^1 \to C$, the vector bundle $f^*T(X)$ decomposes as $O(2) + O(1)^p + O^q$ for some nonnegative integers satisfying $p+q=\dim X -1$. For a Fano manifold $X$ of Picard number 1, a general rational curve of minimal degree through a general point is standard. It has been asked whether all rational curves of minimal degree through a general point are standard. In a joint work with Hosung Kim, we find a negative example to this question. Let $d >2$ be an odd integer and let $f(x_1,..., x_n, x_{n+1})$, $n > d-1$, be a weighted homogeneous polynomial of degree $2d$ with respect to the weights $wt(x_1)=...= wt(x_n) =1$ and $wt(x_{n+1}) =2$. Let $X^f$ be a Veronese double cone of dimension $n$ associated to a general choice of $f$. This is an $n$-dimensional Fano manifold of Picard number 1 with index $n+2-d$. We study the variety of minimal rational tangents at a general point $x$ of $X^f$, the projective variety defined as the union of the tangent directions to rational curves of minimal degree through $x$. We show that the normalization morphism of the variety of minimal rational tangents is not an immersion if $2d < n+1$, which implies that some rational curves of minimal degree through $x$ are not standard.

"Degree Complexity: How difficult is it to compute Groebner bases?" by Ahn (20140221_KIAS.pdf).

: How difficult is it to compute Gr\"{o}bner Bases? Since the construction of Gr\"{o}bner bases provides the foundation for most computation in algebraic geometry and commutative algebra, it is important to know the complexity of the computation of Gr\"{o}bner Bases. For a homogeneous ideal $I$ in a polynomial ring $R=k[x_0,\ldots, x_n]$, Bayer and Mumford introduced the regularity of the initial ideal of $I$ with respect to a term order  $\tau$ as a measure of the complexity of computing Gröbner bases. One of the important problems is to bound the regularity of an initial ideal of $I$ for a given term order $\tau$ on monomials. Two typical orderings are the graded lexicographic ordering and the graded reverse lexicographic order. Many people have studied this problem with respect to the reverse lexicographic term ordering, as these ideals have essentially best-case complexity due to a result of Bayer and Stillman. However, much less is known about regularities of initial ideals with respect to the lexicographic term ordering. One expects them to require many more generators than the reverse lexicographic initial ideals, but their precise behavior has been very little known. In this talk, I will give a survey of the recent progress on this topic and introduce a relationship between the complexity of algebraic computations with the ideal of a smooth variety and the geometry of its generic projection.

"A tropical characterization of an analytic variety to be algebraic" by Nisse.

: All tools will be defined in this talk with sample examples. Amoebas are images of subvarieties of the complex algebraic torus under the coordinatewise logarithm map. G. Bergman introduced the logarithmic limit set $\mathscr{L}^{\infty}(V)$ of a subvariety $V$ of the torus as the set of limiting directions of points in its amoeba. Bieri and Groves showed that if $V$ is algebraic, then $\mathscr{L}^{\infty}(V)$ is a finite rational polyhedral complex of dimension $\dim_{\mathbb{C}}(V) - 1$ in the sphere $S^{n-1}$. Logarithmic limit sets are now called tropical varieties. We show that a generic $k$-dimensional analytic subvariety of the $n$-dimensional complex torus is algebraic if and only if its logarithmic limit set is a finite rational complex polyhedral of dimension $k-1$. In particular, if the dimension of the ambient space is at least $2k$, then the last conditions are equivalent to the fact that the volume of the amoeba is finite. I will focus my talk on the main idea behind this result by showing some concrete examples of holomorphic curves.

"m-dissimilarity tensors and graphs of genus 1" by Bocci (talk_Korea.pdf).

: In this talk I will introduce two results (joint works with Filip Cools, University of Leuven) based on tropical techniques for the study of phylogenetic inference. In particular I will show a complete description, in term of tropical equations, of space of m-dissimilarity tensors (which arise naturally in the study of DNA chains) and a further results on graphs of genus 1 which represent, in biology, particular cases of speciation.

Map and direction for CMC:

*Address: Korea University Alumni Association Bdlg. 13 Jongam-ro, Seongbuk-gu, Seoul 136-712, Korea