Minicourse: General relativity in spherical symmetry


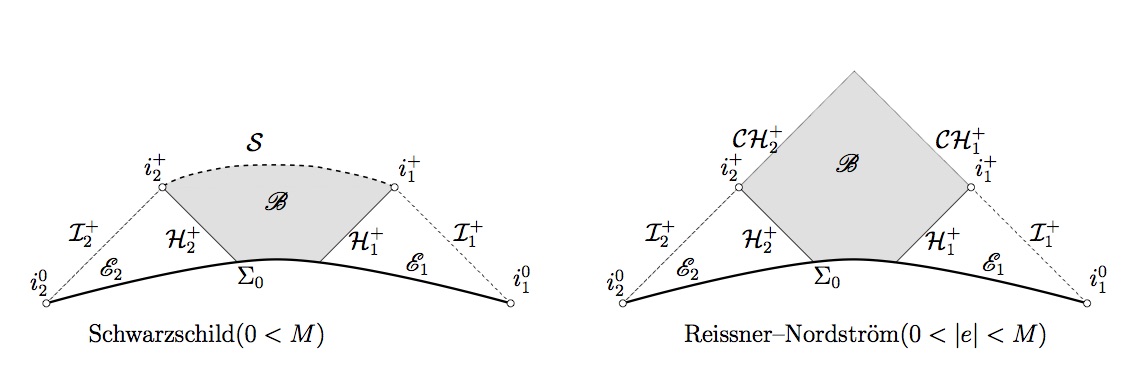
The first part of this mini-course will be an introduction to general relativity in the simplified setting of spherical symmetry, which allows one to penetrate quickly to the heart of the matter with little technical distractions. Then in the second part, an exposition of the recent proof of the strong cosmic censorship conjecture for the Einstein-Maxwell-Scalar-Field model in spherical symmetry will be given.

Schedule

We will meet every Friday (4/7, 4/14, 4/21, 4/28) in KIAS, Rm 8309
from 10:30 am to 12:30 pm and 1:30 pm to 3:30 pm.

Topics (tentative)
1 Basic Lorentzian Geometry
2 Einstein's gravitational field equation and the initial value formulation
3 Vacuum Einstein's equation in spherical symmetry: Birkhoff's theorem and the Schwarzschild spacetime
4 Penrose diagram and a-priori characterization of the causal boundary
5 Strong cosmic censorship for the Einstein-Maxwell-Scalar-Field system (Dafermos's model) in spherical symmetry, Part 1: Linear case
6 Strong cosmic censorship for the Einstein-Maxwell-Scalar-Field system (Dafermos's model) in spherical symmetry, Part 2: Nonlinear analysis in the black hole interior
7 Strong cosmic censorship for the Einstein-Maxwell-Scalar-Field system (Dafermos's model) in spherical symmetry, Part 3: Nonlinear Price's law theorem
8 Strong cosmic censorship for the Einstein-Maxwell-Scalar-Field system (Dafermos's model) in spherical symmetry, Part 4: Nonlinear analysis in the black hole exterior
References
1 V. Schlue, Lecture on General Relativity
(http://www.ljll.math.upmc.fr/~schlue/grt.pdf) [General reference]
2 H. Ringström, The Cauchy problem in General Relativity
[For Lectures 1 and 2]
3 M. Dafermos, Spherically symmetric spacetimes with a trapped surface (http://arxiv.org/abs/gr-qc/0403032) [for Lecture 4]
4 J. Luk and S.-J. Oh, Proof of linear instability of the Reissner-Nordström Cauchy horizon under scalar perturbation (http://arxiv.org/abs/1501.04598) [for Lecture 5]
5 M. Dafermos and I. Rodnianski, A proof of Price's law for the collapse of a self-gravitating scalar field (http://arxiv.org/abs/gr-qc/0309115) [for Lecture 6]
6 J. Luk and S.-J. Oh, Strong cosmic censorship in spherical symmetry for two-ended asymptotically flat initial data I and II (http://arxiv.org/abs/1702.05715, http://arxiv.org/abs/1702.05716) [for Lectures 7 and 8]

Back to main page