

Eli Yablonovitch (UCLA, USA)
Presentations: Click_Here_1



http://www.ee.ucla.edu/faculty/bios/yablonovitch.htm
Eli Yablonovitch graduated with the Ph. D. degree in Applied Physics from Harvard University in 1972. He worked for two years at Bell Telephone Laboratories, and then became a professor of Applied Physics at Harvard. At the peak of the energy crisis in 1979, he joined Exxon to do research on photovoltaic solar energy. Then in 1984, he joined Bell Communications Research, where he was a Distinguished Member of Staff, and also Director of Solid-State Physics Research. In 1992 he joined the University of California, Los Angeles, where he is Professor of Electrical Engineering.
Prof. Yablonovitch has received the Julius Springer Prize in Applied Physics, 2001, "for the impact of photonic crystals on basic research, as well as on a great variety of applications", the R. W. Wood Prize of the Optical Society of America, 1996, "for proposing the concept of Photonic Crystals and electromagnetic band structure engineering", the W. Streifer Scientific Achievement Award of the IEEE/LEOS, 1993 "for contributions to opto-electronics, including the physics of strained-layer lasers and photonic applications of low dimensional structures", and the Adolf Lomb Medal of the Optical Society of America, 1978.
Yablonovitch was the Clifford Paterson Lecturer of the Royal Society of London, 2000, a Founder of the W/PECS series of Photonic Crystal International Workshops that began in 1999, (PECS III was held in Scotland in 2001), and he was an Alfred P. Sloan Fellow, 1978-79.
He is a Fellow of the Institute of Electrical and Electronic Engineers, the Optical Society of America, and the American Physical Society, and a Life Member of eta kappa nu..
His work has covered a broad variety of topics: nonlinear optics, laser-plasma interaction, infrared laser chemistry, photovoltaic energy conversion, strained-quantum-well lasers, and chemical modification of semiconductor surfaces. Currently his main interests are in optoelectronics, high speed optical communications, high efficiency light-emitting diodes and nano-cavity lasers, photonic crystals at optical and microwave frequencies, quantum computing and quantum communication.
Talks:
1. Introduction to Experimental Implementations of Quantum Computing
2. A Semiconductor Based Teleportation Repeater for Long Distance Quantum Communications
While the promise of quantum information technology is great, the challenge of physically creating such devices and systems is quite substantial. A factorization engine implementing Shor's algorithm is particularly daunting. The error correction required for Shor's algorithm begins to fail for quantum phase errors >10-4 radians, and thousands of nearly perfect quantum gates would be needed. By contrast telecommunication functions, such as quantum key distribution, long distance teleportation, and the quantum repeater, are much more forgiving. A quantum repeater using teleportation can tolerate quantum phase errors as high as 0.1 radians, continuing to function, but at a reduced data rate. Furthermore such a quantum repeater implementing the teleportation algorithm requires only three quantum gates.
Thus the construction of small quantum circuits for teleportation could be a valuable transitional stage to a more advanced technology later. While RSA public key cryptography has no immediate vulnerability, a 3 gate quantum repeater for long distance key distribution would still be a useful initial stepping stone to a later world of more complex telecommunications circuits, and ultimately to factorization engines.
Useful quantum circuits still seem very distant, but there are a large number of material systems, atoms, ions, flux and charge qubit superconductors, and semiconductor spins, that are being investigated for their ability to safely preserve quantum mechanical phase angles. While the road ahead is still fraught with risks, history has shown that the progress of semiconductor technology is relentless. Nature has been particularly kind to Silicon. The electron spin in Silicon is exceptionally robust. It preserves its quantum phase information for a time period close to 1 milli-second (the homogeneous T2 dephasing time). Indeed there are standard procedures, like isotope purification and nuclear spin de-coupling that would increase that lifetime to >1msec. Small transistors have already been made that are sensitive to single electric charges, and some transistors are sensitive to an ensemble of spins.
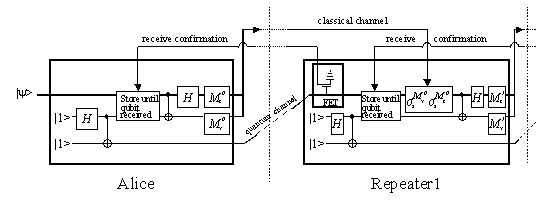
Figure 1: The first two stages of a quantum repeater system, that can faithfully transmit quantum information over long distances, in spite of fiber attenuation.
One of the best ways of transmitting a quantum state is in the polarization state of a photon. If supplemented with birefringence compensation, the existing network of classical optical communications fibers could be readily adaptable for this purpose. Such photon states could serve to distribute quantum cryptographic keys, but the transmission range would be limited by the fiber attenuation length. Quantum states being notoriously fragile, they cannot survive destruction in the fiber. Amazingly, however, it is possible to make a repeater that transmits the photon quantum state with high confidence, in spite of a substantial probability of absorption in the fiber. The device that does this is called a quantum repeater, and is illustrated in Fig. 1.
The quantum repeater operates on the basis of the teleportation algorithm, but there is an added feature that makes it robust against photon loss. At the input of the repeater there is a field effect transistor, (FET), that senses the charge of a photo-electron, without disturbing the electron's spin polarization state. Such an FET acts as a photo-detector that has the new property of transferring the photon polarization state directly to the photo-electron spin polarization state. The polarization selection rules for doing this were introduced in ref.. The key point is the photo-detector FET detects charge, but does not disturb11 spin.
An essential capability for quantum opto-electronics, is to inter-convert information back and forth, to/from photons and electrons. Fortunately there are selection rules linking photon polarization (or angular momentum) with electron spin polarization that arises from the angular momentum of the semiconductor bands. The top of the GaAs valence band is composed of mj=±3/2 wave functions, while the bottom of the conduction band is s-like and contains only ms=±1/2 wave functions. A circularly polarized photon beginning from mj= -3/2, can couple only to the pure ms= -1/2 state. Thus the transfer of a specific photon polarization to a single electron spin polarization is readily achieved. While such a pure electron spin polarization may be easily optically produced, and optically detected, such a electron spin polarization is unusable for quantum communication and processing. To take advantage of the quantum degrees of freedom, both electron spin polarizations must be accessible simultaneously, spanning the full electron spin Hilbert space.
References:
1. Biham, E.; Boyer, M.; Boykin, P.O.; Mor, T.; Roychowdhury, V. A proof of the security of quantum key distribution. Proceedings of the Thirty Second Annual ACM Symposium on Theory of Computing, STOC'00 Portland, OR, USA, 21-23 May 2000. p.715-24.
2. J. Hald, J. L. Sorensen, C. Schori, and E. S. Polzik, ¡°Spin Squeezed Atoms: A Macroscopic Entangled Ensemble Created by Light¡±, Phys. Rev. Lett., vol. 83 (1999) pp. 1319 - 1322.
3. D. Kielpinski, V. Meyer, M. A. Rowe, C. A. Sackett, W. M. Itano, C. Monroe, D. J. Wineland, ¡°A Decoherence-Free Quantum Memory Using Trapped Ions¡±, Science, vol. 291 (2001) pp. 1013 - 1015.
4. J. E. Mooji, T. P. Orlando, L. Levitov, Lin Tian, Casper H. van der Wal, Seth Lloyd, ¡°Josephson Persistent-Current Qubit", Science, vol. 285 (1999) pp. 1036 - 1039. J. R. Friedman, V. Patel, W. Chen, S. K. Tolpygo and J. E. Lukens, ¡°Quantum superposition of distinct macroscopic states", Nature, vol. 406 (2000) pp. 43 - 46.
5. Y. Nakamura, Yu. A. Pashkin and J. S. Tsai, ¡°Coherent control of macroscopic quantum states in a single-Cooper-pair box¡±, Nature, vol. 398 (1999) pp. 786 - 788.
6. B.E. Kane, ¡°A Silicon Based Nuclear Spin Quantum Computer¡±, Nature 393, 133 (1998).
7. ¡°Principles of Magnetic Resonance, 3rd ed.¡± C. P. Slichter, (Springer, Berlin, 1996). See especially p. 303.
8. Bethune, D.S.; Risk, W.P. An autocompensating fiber-optic quantum cryptography system based on polarization splitting of light. IEEE Journal of Quantum Electronics, vol.36, (no.3), March 2000. p.340-7.
9. Richard J. Hughes, Williams T. Buttler, Paul G. Kwait, Steve K. Lamoreaux, George L. Morgan, Jane E. Nordholt and C. Glen Peterson, ¡°Practical quantum cryptography for secure free-space communications¡±, http://xxx.arxiv.org/abs/quant-ph/9905009.
10. Cirac, J.I.; Zoller, P.; Kimble, H.J.; Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Physical Review Letters, vol.78, (no.16), APS, 21 April 1997. p.3221-4.
11. Vrijen, R.; Yablonovitch, E. A spin-coherent semiconductor photodetector for quantum communication. Physica E, vol.10, (no.4), Elsevier, June 2001. p.569-75.