WHY IS THE PERSON IN A PHOTO LOOKING AT US NO MATTER WHERE WE ARE?

One day I had dinner with the graduating students in a farewell party at Seoul National University. After dinner we went to a beerhouse. While we were talking a lot there I saw a big photo of an attractive girl in swimsuit on the wall. She was gazing at me with a seductive smile. All of a sudden, a good mathematical idea sprang to my mind. With a smile of excitement I asked a question to the students.
“Why is that girl staring at me all the time?”
There was a burst of laughter. But a student did not agree and said,
“She is looking at me as well.”
So I asked another question more appropriate from a teacher.
“Why is that girl looking at everyone in this hall?”
And I added like a math professor.
“Why is the person in a photo looking at us no matter where we are?”
All the students took it for granted. They were so accustomed to it. The only answer I got was that it is because the photo is on a plane. So I gave a last math lecture to the graduating students about the attractive girl in swimsuit. .

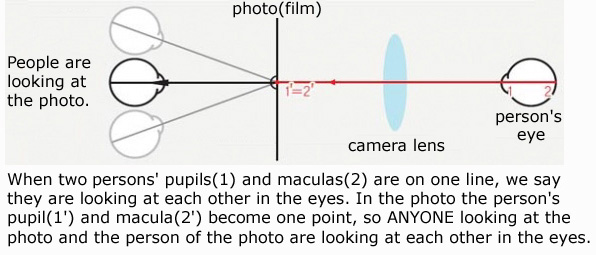
The answer to this question comes from elementary geometry. Everyone has his or her line of sight. The line of sight is the line determined by the pupil and the macula of a person. The macula, or the yellow spot, is the center of the retina of the eye. So the line of sight is like a line in Euclidean geometry, which is uniquely determined by two points in space. The light passes through a person’s pupil and then stimulates the optic nerves on his or her retina. While we are living in three dimensional space, the human lines of sight travel to and fro in space. When two lines of sight overlap and coincide with one another we say that the two people are looking each other in the eye.

When one takes a picture of a woman, she gazes at the lens of the camera, and so the lens lies on her line of sight. But the line of sight of the woman in the resulting photo becomes a point. This is because the picture-taking is the job of projecting the lines through the lens onto the points of the photo. As a result, the camera transforms the three-dimensional space into a two-dimensional picture. Therefore, the line of sight gazing into the camera reduces to a point.

The clue here is that the reduced point is actually the double point overlapped by the woman’s pupil and macula. Therefore, any line emanating from this point becomes the line of sight of the woman in the photo. Consequently the woman is gazing in all directions. So when we are looking at this double point, no matter where we are, our line of sight coincides with hers, and hence we feel that she is gazing at us. The mathematical core of this phenomenon is that two distinct points determine only one line, while there are infinitely many lines passing through a double point. This is why the person in a photo can gaze at us wherever we are.



What about the woman in the second photo? She does not look into our eyes no matter where we move. The reason is the following. When she does not look at the camera, her pupil and macula do not overlap in her photo. So her line of sight becomes only one line, but unfortunately, this line lies in the plane of photo. Therefore she cannot look at us. We could force her to gaze at us if we put our eyes on the plane of photo. But then her picture would become a one-dimensional line and hence would be unrecognizable.

These strange phenomena occur due to the forced projection of a three-dimensional person onto a two-dimensional photo. The reduction of the dimension is the cause. There is an 1884 classic novella called Flatland written by the English schoolmaster Edwin A. Abbott about the two-dimensional world. It tells of a heuristic encounter of a two-dimensional Square with a three-dimensional Sphere. The Square is visited by the Sphere, who teaches him unbelievable facts about Spaceland and even tells him that from space one can see his insides such as the stomach. Bewildered, the Square does not believe the Sphere.

So the Sphere takes the Square to Spaceland to show him the extra dimension, and eventually the Square’s mind is opened to new dimensions. Taking a step forward, the Square tries to convince the Sphere of the theoretical possibility of the existence of more spacious space, the four-dimensional space. From there, the Square wishes to see the interior of the Sphere, his intestines. Offended by the Square’s presumption and incapable of comprehending the fourth dimension, the Sphere returns the Square to Flatland in disgrace.

Just like the inhabitants of Abbott’s Pointland, Lineland, Flatland and Spaceland, humans are sometimes averse to expanding their horizons, and to imagining what lies beyond the boundaries of their knowledge. Though it is difficult to go into higher dimensions, lower dimensions are easy to put in perspective. Every human being lives in four-dimensional space-time, skillfully handling and quickly analyzing thousand pieces of three-dimensional, two-dimensional and one-dimensional information that originate from the four-dimensional phenomena. In this way, however, we oversimplify a three-dimensional person into a two-dimensional image on a photo, and as a result, the person in the photo is looking at us no matter where we are.


Jaigyoung Choe
Korea Institute for Advanced Study
choe@kias.re.kr
http://newton.kias.re.kr/~choe