등주부등식 (等周不等式, Isoperimetric Inequality)
평면 위에서 닫힌 곡선 C의 길이를 L이라 하고 그 내부의 넓이를 A라 하면 모든 C에 대해 4 pi A <= L^2 이라는 등주부등식이 성립한다. 여기서 등식이 만족되기 위한 필요충분 조건은 곡선 C가 원일 경우이다.
 등주부등식의 역사는 지금부터 2,800년
전 고대 그리스 시대에 시작되었다. 페니키아의
폭군 피그말리온의 여동생 디도 여왕은 폭정을 피해 국외로 망명하여 카르타고에 정착하게
되었다. 그 곳의 원주민들은 디도여왕에게 쇠가죽을 주어서 그것으로 둘러쌀 수 있는 넓이의
땅만 그녀에게 팔겠다고 하였다. 디도여왕은 그것을 잘게 썰어 긴 끈으로 이은 다음 이 끈으로
자기 땅의 경계를 만들었는데, 정작 그녀가 만든 경계는 정사각형이 아니고 원이었다. 이것으로
보아 총명한 디도여왕은 주어진 길이의 곡선 중에서 가장 큰 넓이를 둘러싸는 것은 원이라는
수학적 사실을 경험을 통해서 안 것으로 여겨진다. 그러나 이 디도여왕의 문제, 즉 등주부등식
문제의 엄밀한 증명은 19세기에 들어와서야 Steiner에 의해 우여곡절 끝에 이루어졌다. 그의
방법은 2차원 평면 뿐만 아니라 모든 차원의 유클리드 공간에도 적용되므로 주어진 넓이의
(n-1)차원 닫힌 곡면 중 가장 큰 부피를 둘러싸는 것은 n차원 공이라는 좀 더 일반적인 사실이
성립하게 된다.
등주부등식의 역사는 지금부터 2,800년
전 고대 그리스 시대에 시작되었다. 페니키아의
폭군 피그말리온의 여동생 디도 여왕은 폭정을 피해 국외로 망명하여 카르타고에 정착하게
되었다. 그 곳의 원주민들은 디도여왕에게 쇠가죽을 주어서 그것으로 둘러쌀 수 있는 넓이의
땅만 그녀에게 팔겠다고 하였다. 디도여왕은 그것을 잘게 썰어 긴 끈으로 이은 다음 이 끈으로
자기 땅의 경계를 만들었는데, 정작 그녀가 만든 경계는 정사각형이 아니고 원이었다. 이것으로
보아 총명한 디도여왕은 주어진 길이의 곡선 중에서 가장 큰 넓이를 둘러싸는 것은 원이라는
수학적 사실을 경험을 통해서 안 것으로 여겨진다. 그러나 이 디도여왕의 문제, 즉 등주부등식
문제의 엄밀한 증명은 19세기에 들어와서야 Steiner에 의해 우여곡절 끝에 이루어졌다. 그의
방법은 2차원 평면 뿐만 아니라 모든 차원의 유클리드 공간에도 적용되므로 주어진 넓이의
(n-1)차원 닫힌 곡면 중 가장 큰 부피를 둘러싸는 것은 n차원 공이라는 좀 더 일반적인 사실이
성립하게 된다. 한편 평면에서 이 등주부등식 문제가 해결된 뒤 수학자들은 이것을 곡면으로 확장하는 문제를 연구하기 시작하였다. 그리하여 1933년에 Rado는 곡면이 영 또는 음의 곡률을 갖고 단순연결일 때 그 곡면 위에 있는 닫힌 곡선의 길이와 내부의 넓이에 대해 4 pi A <= L^2 이 성립함을 보였다. 여기서 곡면이 단순연결이라는 가정이 필수적이다. 왜냐하면 긴 원통의 굽어진 표면을 주어진 곡면으로 삼으면 그 경계는 두 개의 원으로서 길이가 고정돼 있으나 그 곡면의 내부의 넓이는 원통이 길수록 커지므로 등주부등식을 만족할 수 없게 된다.
 그러나
이러한 단순연결이라는 가정이 없어도 여전히 등주부등식이 성립하는 곡면은 존재할
것인가? 이 곡면을 찾으려면 등주부등식이 성립하는 평면의 성질을 여전히 갖고 있는 곡면을
우선 찾아야 할 것이다. 수많은 곡면중에 극소곡면이라는 게 있다. 이것은 평균곡률이 영인
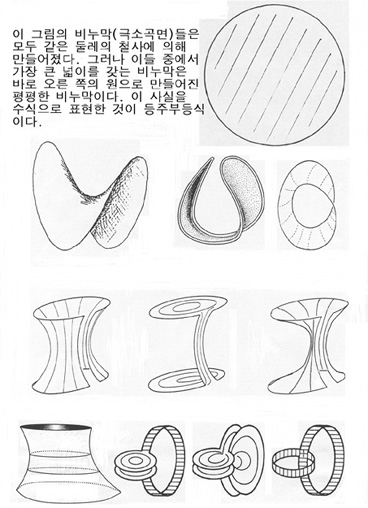
곡면인데 쉬운 예로 모든 비누막은 극소곡면이다. 철사고리를 비눗물에 담갔다 꺼내면 비누막이
생기는데 이 비누막은 주어진 철사고리를 경계로 하는 모든 곡면 중에서 넓이가 가장 작은
곡면이다. 쉽게 얘기해서 넓이가 최소이면 넓이의 미분계수(=평균곡률)가 영이 되므로 이로부터
극소곡면의 정의가 생기는 것이다. 철사고리가 평면 위에 있는 곡선이라면 이 철사고리로 생기는
비누막은 바로 평면의 일부가 되니까 평면은 극소곡면이 된다. 그래서 극소곡면은 평면을
일반화한 곡면으로 볼 수 있는 것이다. 여기서 극소곡면에 대한 등주부등식 문제가 제기된다.
유한한 경계를 갖는 극소곡면은 과연 4 pi A <= L^2 을 만족할 것인가?
이 문제는 20세기 초에 제기되었으나 아직 완전히 해결되지는 않았고 부분적인 해결만
이루어졌다. 1921년에 Carleman은 극소곡면이 단순연결일 때 등주부등식을 증명하였고,
1970년대에 이중연결인 극소곡면에 대해, 1980년대에는 경계의 개수가 2개이고 3차원 공간 속에
있는 극소곡면에 대해 등주부등식이 증명되었다.
그러나
이러한 단순연결이라는 가정이 없어도 여전히 등주부등식이 성립하는 곡면은 존재할
것인가? 이 곡면을 찾으려면 등주부등식이 성립하는 평면의 성질을 여전히 갖고 있는 곡면을
우선 찾아야 할 것이다. 수많은 곡면중에 극소곡면이라는 게 있다. 이것은 평균곡률이 영인
곡면인데 쉬운 예로 모든 비누막은 극소곡면이다. 철사고리를 비눗물에 담갔다 꺼내면 비누막이
생기는데 이 비누막은 주어진 철사고리를 경계로 하는 모든 곡면 중에서 넓이가 가장 작은
곡면이다. 쉽게 얘기해서 넓이가 최소이면 넓이의 미분계수(=평균곡률)가 영이 되므로 이로부터
극소곡면의 정의가 생기는 것이다. 철사고리가 평면 위에 있는 곡선이라면 이 철사고리로 생기는
비누막은 바로 평면의 일부가 되니까 평면은 극소곡면이 된다. 그래서 극소곡면은 평면을
일반화한 곡면으로 볼 수 있는 것이다. 여기서 극소곡면에 대한 등주부등식 문제가 제기된다.
유한한 경계를 갖는 극소곡면은 과연 4 pi A <= L^2 을 만족할 것인가?
이 문제는 20세기 초에 제기되었으나 아직 완전히 해결되지는 않았고 부분적인 해결만
이루어졌다. 1921년에 Carleman은 극소곡면이 단순연결일 때 등주부등식을 증명하였고,
1970년대에 이중연결인 극소곡면에 대해, 1980년대에는 경계의 개수가 2개이고 3차원 공간 속에
있는 극소곡면에 대해 등주부등식이 증명되었다.이상은 등주부등식의 간략한 역사이다. 이제부터 내 이야기를 시작해 보자. 학위를 취득한지 이태 째인 1987년 여름부터 1년간 나는 Berkeley에 있는 수학연구소 MSRI에 Postdoctor로 있었다. 그 전해부터 나는 학위논문 이후의 논문 문제를 여기저기서 찾아보느라 고심하던 중이었다.
 나에게 재미있는 문제로서, 풀릴 수 있고, 또 많은 사람이 관심을 가질 수 있어야
한다는 세가지 조건을 만족하는 문제를 찾기란 참 어려운 일이었다. 이 과정에서 흥미를 갖게된
게 극소곡면의 등주부등식 문제였다. 해석적인 수식들로부터 재미있는 기하학적인 사실들을
이끌어내는 증명과정이 무척 아름답다고 느껴졌었다.
최상의 연구여건을 갖춘 MSRI에서 처음
6개월간 아무 연구성과가 없다 보니 스트레스가 이만저만 쌓이는 게 아니었다. 이런 상황속에
시작한 극소곡면의 등주부등식 문제는 즐거운 연구대상이었고 결국 어려움을 극복하는 계기가
되었다. 이 문제를 위해 나는 다음과 같은 기하학적인 아이디어를 썼다. 즉 주어진 극소곡면과
같은 경계를 갖는 가우스곡률 0인 곡면(cone)의 넓이보다 극소곡면의 넓이가 작다는 “넓이
비교식”을 이끌어 내고, 이로부터 극소곡면의 등주부등식을 평면 위의 등주부등식으로
귀착시켰다. 이리하여 극소곡면의 경계가 두개만 있을 경우에 등주부등식을 증명한 것이다.
여기서 한 걸음 더 나아가 극소곡면의 넓이 비교식에서 등식이 성립하는 경우가 geodesic의
conjugate point와 대응된다는 사실을 깨닫고 이로부터 Morse index 정리를 극소곡면으로
확장할 수 있게 되었다.
나에게 재미있는 문제로서, 풀릴 수 있고, 또 많은 사람이 관심을 가질 수 있어야
한다는 세가지 조건을 만족하는 문제를 찾기란 참 어려운 일이었다. 이 과정에서 흥미를 갖게된
게 극소곡면의 등주부등식 문제였다. 해석적인 수식들로부터 재미있는 기하학적인 사실들을
이끌어내는 증명과정이 무척 아름답다고 느껴졌었다.
최상의 연구여건을 갖춘 MSRI에서 처음
6개월간 아무 연구성과가 없다 보니 스트레스가 이만저만 쌓이는 게 아니었다. 이런 상황속에
시작한 극소곡면의 등주부등식 문제는 즐거운 연구대상이었고 결국 어려움을 극복하는 계기가
되었다. 이 문제를 위해 나는 다음과 같은 기하학적인 아이디어를 썼다. 즉 주어진 극소곡면과
같은 경계를 갖는 가우스곡률 0인 곡면(cone)의 넓이보다 극소곡면의 넓이가 작다는 “넓이
비교식”을 이끌어 내고, 이로부터 극소곡면의 등주부등식을 평면 위의 등주부등식으로
귀착시켰다. 이리하여 극소곡면의 경계가 두개만 있을 경우에 등주부등식을 증명한 것이다.
여기서 한 걸음 더 나아가 극소곡면의 넓이 비교식에서 등식이 성립하는 경우가 geodesic의
conjugate point와 대응된다는 사실을 깨닫고 이로부터 Morse index 정리를 극소곡면으로
확장할 수 있게 되었다.  이 다음 자연스럽게 제기되는 것은 비유클리드 공간 속의
극소곡면에 대해서도 넓이 비교식과
등주부등식이 성립할 것인가 하는 문제이다. 그런데 1988년 여름부터 나는 텍사스에 있는 Rice
대학에서 가르치게 되었다. 여기서 등주부등식 논문과 Morse index 논문을 마무리 지었다. 큰
고비를 넘긴 셈이었다. 그리고 1989년 여름 석달간 Bonn대학에 가족과 함께 방문하였다. 여기서
이국적인 분위기 속에 MSRI에서 처럼 맘껏 연구에만 전념할 수 있었다. 이때 Morse index 정리에
관심을 가진 미네소타 대학의 Gulliver를 만나게 되었다. 그의 초청으로 그해 11월에 닷새 동안
미네소타 대학을 방문하여 Colloquium talk을 하였다. 이 닷새간 우리는 넓이 비교식을
비유클리드 공간 속의 극소곡면에 대해 증명하려 했지만 성공하지 못하였다. 그러나 적절히
수정된 넓이에 대한 비교식은 얻을 수 있었고 따라서 이 수정된 넓이에 대한 등주부등식을
특수한 경우에 대해 증명할 수 있었다. 한달 후 Austin에 있는 텍사스 대학에서 학회가 열렸는데
여기서 나는 등주부등식, Morse index 정리, 수정된 등주부등식에 관해 발표하였다. 이때 청중
속의 두 사람이 나에게 다음과 같은 사실을 알려주었다. 한 사람은 Russia의 수학자
Alexandrov의 제자인 Bakelman이었는데 그는 나의 넓이 비교식과 Alexandrov의 한 결과 사이의
연관성을 일깨워 주었다. Wei라는 다른 한 사람은 Simon이 유클리드 공간 속의 모든 극소곡면에
대해 다소 완화된 등주부등식 2 pi A <= L^2 을 아무 조건 없이 증명하였다고 말해
주었다. 며칠 후 Wei가 Simon의 논문을 보내 주었는데 그 증명은 간단하면서도 매우 아름다웠다.
해석학과 기하학을 절묘하게 결합시킨 정리였다.
이 다음 자연스럽게 제기되는 것은 비유클리드 공간 속의
극소곡면에 대해서도 넓이 비교식과
등주부등식이 성립할 것인가 하는 문제이다. 그런데 1988년 여름부터 나는 텍사스에 있는 Rice
대학에서 가르치게 되었다. 여기서 등주부등식 논문과 Morse index 논문을 마무리 지었다. 큰
고비를 넘긴 셈이었다. 그리고 1989년 여름 석달간 Bonn대학에 가족과 함께 방문하였다. 여기서
이국적인 분위기 속에 MSRI에서 처럼 맘껏 연구에만 전념할 수 있었다. 이때 Morse index 정리에
관심을 가진 미네소타 대학의 Gulliver를 만나게 되었다. 그의 초청으로 그해 11월에 닷새 동안
미네소타 대학을 방문하여 Colloquium talk을 하였다. 이 닷새간 우리는 넓이 비교식을
비유클리드 공간 속의 극소곡면에 대해 증명하려 했지만 성공하지 못하였다. 그러나 적절히
수정된 넓이에 대한 비교식은 얻을 수 있었고 따라서 이 수정된 넓이에 대한 등주부등식을
특수한 경우에 대해 증명할 수 있었다. 한달 후 Austin에 있는 텍사스 대학에서 학회가 열렸는데
여기서 나는 등주부등식, Morse index 정리, 수정된 등주부등식에 관해 발표하였다. 이때 청중
속의 두 사람이 나에게 다음과 같은 사실을 알려주었다. 한 사람은 Russia의 수학자
Alexandrov의 제자인 Bakelman이었는데 그는 나의 넓이 비교식과 Alexandrov의 한 결과 사이의
연관성을 일깨워 주었다. Wei라는 다른 한 사람은 Simon이 유클리드 공간 속의 모든 극소곡면에
대해 다소 완화된 등주부등식 2 pi A <= L^2 을 아무 조건 없이 증명하였다고 말해
주었다. 며칠 후 Wei가 Simon의 논문을 보내 주었는데 그 증명은 간단하면서도 매우 아름다웠다.
해석학과 기하학을 절묘하게 결합시킨 정리였다.1990년 봄학기를 바삐 가르치며 보낸 뒤 나는 9년간의 미국생활을 청산하였다. 이쯤 되면 한국에서도 혼자 연구생활을 계속할 수 있겠다는 느낌이 들어서였다. 6월에 포항공대에 부임한 뒤 새로운 환경에 적응하면서 나는 비유클리드 공간 속에 있는 극소곡면의 등주부등식 문제를 다시 연구하기 시작하였다. 그러나 유클리드 공간과 비유클리드 공간의 차이는 쉽게 건너뛸 수 있는 성질의 것이 아니었다. 별 진전 없이 한 학기가 지나갔고 학기말에는 학생들의 시험거부 소요사태로 학교의 분위기가 매우 산만하였다. 학기가 끝나고 조용해지자 연구에 진전이 조금씩 있더니 드디어 Simon의 등주부등식을 비유클리드 공간 속의 극소곡면으로 확장할 수 있게 되었다. 이때 얻은 결과와 1년전에 Gulliver와 함께 얻은 수정된 등주부등식에 관한 논문을 쓰며 그해 연말연시는 즐거움 속에 보냈다. 이 논문은 Gulliver와의 공동논문으로 독일의 학술지에 실렸다.
 Simon처럼 완화하지는 않은 원래의 등주부등식을 얻으려면 비유클리드
공간에서 넓이 비교식을
증명해야 한다. 그리고 이 비교식을 보이려면 곡면의 성질을 적절히 나타내는 함수를 알맞게
정의해야 하는 것이다. 이것은 좀처럼 해결의 실마리가 보이지 않았다. 그러던 어느날 설날이
가까운 1991년 2월 중순이었다. 깊이 잠이든 아이들을 어머니께 부탁하고 아내와 나는 시내
육거리 근처의 다방에 갔다. 아내와 함께 차를 마시던 중 불현 듯 내 머리 속에 산뜻한
아이디어가 떠올랐다. 자정 넘어 집에 돌아와 차근차근 그 아이디어를 계산해 보니 쌍곡적
비유클리드 공간 속의 넓이 비교식이 내 눈 앞에 활짝 모습을 드러내는 게 아닌가! 이와 함께
비유클리드 공간 속에 있는 경계가 두 개인 극소곡면의 등주부등식이 얻어졌다. 그리고 보름 뒤
Gulliver에게서 fax가 왔다. 자기도 등주부등식을 얻었다고. 이리하여 이 결과도 Gulliver와의
공동논문으로 쓰여졌고 곧 독일의 학술지에 실렸다.
Simon처럼 완화하지는 않은 원래의 등주부등식을 얻으려면 비유클리드
공간에서 넓이 비교식을
증명해야 한다. 그리고 이 비교식을 보이려면 곡면의 성질을 적절히 나타내는 함수를 알맞게
정의해야 하는 것이다. 이것은 좀처럼 해결의 실마리가 보이지 않았다. 그러던 어느날 설날이
가까운 1991년 2월 중순이었다. 깊이 잠이든 아이들을 어머니께 부탁하고 아내와 나는 시내
육거리 근처의 다방에 갔다. 아내와 함께 차를 마시던 중 불현 듯 내 머리 속에 산뜻한
아이디어가 떠올랐다. 자정 넘어 집에 돌아와 차근차근 그 아이디어를 계산해 보니 쌍곡적
비유클리드 공간 속의 넓이 비교식이 내 눈 앞에 활짝 모습을 드러내는 게 아닌가! 이와 함께
비유클리드 공간 속에 있는 경계가 두 개인 극소곡면의 등주부등식이 얻어졌다. 그리고 보름 뒤
Gulliver에게서 fax가 왔다. 자기도 등주부등식을 얻었다고. 이리하여 이 결과도 Gulliver와의
공동논문으로 쓰여졌고 곧 독일의 학술지에 실렸다.이상은 내가 등주부등식 문제에 접하게 된 경위를 간단히 적어 본 것이다. 등부주등식은 내가 좋아하는 몇가지 문제 가운데 하나이다. 요즘도 때때로 이 문제를 생각하곤 한다. 며칠 전에는 이 등주부등식 문제를 완전히 풀었는 줄 알았다. 그러나 곧 그것은 착각임이 드러났다. 이런 착각은 지난 12년간 아마도 백번 넘어 경험해 봤으리라. 그러나 이렇게 아끼고 즐기는 문제가 있고 또 짧은 순간이나마 황홀한 착각을 종종 맛볼 수 있는 한 앞으로도 항상 박진감 있고 희열이 넘치는 연구생활을 계속하게 되리라 기대해 본다.
(1996년1월7일씀; 1996년 포항공대 수학과 학생회誌 무한대에 실린 글)